5.5 Instantaneous Rate of Reaction

Its is nothing much to worry about this topic... It is just the same as we studied previously in First Chapter.. RECALL IT..!!

*sorry guys I couldn't able attach with any notes/examples :'(...

Hmmm... Seems to be to the end of chapter. Practice Makes Better..!!! Hope you guys practice alot..CHEEEERRRSsssss!!! :) :)

5.4 Solve Trigonometric Equation :

All about CALculations !!! :)

: http://www.youtube.com/watch?v=IE0FxGegdMg

Example 1:

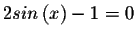
~~$2sin\left( x\right) -1=0$~~
There are an infinite number of solutions to this problem. To solve for x, you must first isolate the sine term.

$\begin{eqnarray*}&& \\ 2\sin \left( x\right) -1 &=&0 \\ && \\ \sin \left( x\right) &=&\displaystyle \frac{1}{2} \\ && \\ && \end{eqnarray*}$

We know that the $\sin \left( \displaystyle \frac{\pi }{6}\right) =\displaystyle \frac{1}{2},$ therefore $x=\displaystyle \frac{\pi }{6}.$ The sine function is positive in quadrants I and II. The $\sin \left( \pi -\displaystyle \frac{\pi }{6}\right) =\sin \displaystyle \frac{5\pi }{6}$ is also equal to $\displaystyle \frac{1}{2}.$ Therefore, two of the solutions to the problem are $x=\displaystyle \frac{\pi }{6}$ and $x=\displaystyle \frac{5\pi }{6}.$

Example 2:

$2\sin\left( 3x\right) -1=0$

There are an infinite number of solutions to this problem. To solve for x, you must first isolate the sine term.

$\begin{eqnarray*}&& \\ 2\sin \left( 3x\right) -1 &=&0 \\ && \\ \sin \left( 3x\right) &=&\displaystyle \frac{1}{2} \\ && \\ && \end{eqnarray*}$

If we restriction the domain of the sine function to $\left[ -\displaystyle \frac{\pi }{2} \leq 3x\leq ,\displaystyle \frac{\pi }{2}\... ...[ -\displaystyle \frac{\pi }{6}\leq x\leq ,\displaystyle \frac{\pi }{6}\right]$ , we can use the inverse sine function to solve for reference angle 3x and then x.

$\begin{eqnarray*}&& \\ \sin \left( 3x\right) &=&\displaystyle \frac{1}{2} \\ &... ...&=&\sin ^{-1}\left( \displaystyle \frac{1}{2 }\right) \\ && \\ \end{eqnarray*}$

$\begin{eqnarray*}3x &=&\sin ^{-1}\left( \displaystyle \frac{1}{2}\right) \\ && ... ...\ x &\approx &0.174532925\ \mbox{ radians }\\ && \\ && \\ && \end{eqnarray*}$

We know that the $\sin$ e function is positive in the first and the second quadrant. Therefore two of the solutions are the angle 3x that terminates in the first quadrant and the angle $\pi -3x$ that terminates in the second quadrant. We have already solved for 3x.

$\begin{eqnarray*}&& \\ \sin \left( \pi -3x\right) &=&\displaystyle \frac{1}{2} ... ...-3x &=&\sin ^{-1}\left( \displaystyle \frac{1}{2}\right) \\ && \end{eqnarray*}$

$\begin{eqnarray*}&& \\ 3x &=&\pi -\sin ^{-1}\left( \displaystyle \frac{1}{2}\ri... ... \\ && \\ x &\approx &0.872665\ \mbox{ radians } \\ && \\ && \end{eqnarray*}$

The solutions are $x=\displaystyle \frac{1}{3}\sin ^{-1}\left( \displaystyle \frac{1}{2}\right)$ and $x=\displaystyle \frac{\pi }{3}-\displaystyle \frac{1}{3}\sin ^{-1}\left( \displaystyle \frac{1}{2}\right) .\bigskip \bigskip\bigskip$
Example 3.
Solve the equation

for 0 ≤ θ < 2π.

Solving for cos θ gives us:

, then the reference angle is α = 1.3181.

So for

, we have θ in the first and 4th quadrants. So

θ = 1.3181 or 4.9651

For

, we have θ in the 2nd and 3rd quadrants. So

θ = 1.8235 or 4.4597

So θ= 1.3181, 1.8235, 4.4597 or 4.9651 radians.

Example 4.
Solve the equation 6 sin²θ − sin θ − 1 = 0 for 0 ≤ θ < 2π.

Factoring the LHS:

6 sin² θ − sin θ − 1 = 0
(2 sin θ − 1)(3 sin θ + 1) = 0

So either

2 sin θ − 1 = 0
sin θ = 1/2
θ will be in 1st and 2nd quadrants.
θ = 0.52360, 2.6180 (ie π/6, 5π/6)

Example 5.
Solve the equation tan 2θ − cot 2θ = 0 for 0 ≤ θ < 2π.

tan²2θ = 1

tan 2θ = ± 1

Since 0 ≤ θ < 2π , we need to consider values of 2θ such that 0 ≤ 2θ < 4π. Hence, solving the above equation, we have:

* For More : http://tutorial.math.lamar.edu/Classes/CalcI/TrigEquations.aspx

5.3 Sinusoidal Functions of the Transformation Form..!!

The transformation of a sine or cosine function f(x) to g(x) has the general form g(x) = a f ( k(x - d) ) + c,
where :

a is the amplitude.
d is the phase shift
c is the vertical translation

The period of the transformed function is given by 2π

5.2 Graphs of Reciprocal Trigonometric Function

The graphs of y = cscx, y = sec x, and y = cot x are periodic. They are related to the graphs of the primary trigonometric functions as reciprocal graphs.

Graph of Cosecant

Cosecant

The Cosecant of an angleis the ratio of length of the hypotenuse and the opposite side.

csc (q) = hypotenuse / Opposite

The cosecant is the inverse of the sine and is given by the relation

csc q = 1 / sin q

Graph of cosecant function:

y = f (x) = csc (x)

Secant Graph.

Secant of an angleis the ratio of length of the hypotenuse and the opposite side.

Sec (q) = hypotenuse / opposite

The secant is the inverse of the sine and is given by the relation
sec q = 1 / cos q

Co-function for secant

Relations between the secant and cosine functions are the co-function of the other.
Sec A = cos (90° - x)

y = f (x) = sec x

Graph of Cotangent .

Below see cotangent function based on right angle triangle -

An angleis the ratio of length of the adjacent side and the length of the opposite side is known as Cotangent.

Cot (q) = adjacent / opposite

It is the inverse of the tangent and its relation is given as

Cot (q ) = 1 / tan q

It is the ratio of cosine and sine functioncan be defined as

Cot (q) = cos q / sin q

Graph for Cotangent function:
y = f (x) = cot x

5.1 Graphs of Sine, Cosine, and Tangent Functions

KeyNotes :

The graphs of y = sin x, y = cos x and y= tan x are periodic.

Sine and Cosine graphs.

The graphs of y = sin x and y = cos x have an amplitude (finding by adding the max. and min. values then dividing by 2) of 1 and a period (a complete cycle) of 2π.

Tangent Graph.

The tan function

The tan function is found using:

It therefore follows that tan θ = 0, when sin θ = 0, and tan θ is undefined when cos θ = 0.

1. This graph is continuous, but is undefined when

2. The range of values for tan θ is unlimited.

3. It has a period of π.

All of the three functions periodically repeat their values and the simplest way to learn this, is to make sure that you understand the general rules below which use 'n' to represent any integer (i.e. any whole number, both positive and negative).

Dawn with Advanced Functions..!!

Saturday, 15 October 2011